Makeup Material for Midterm Exam 1

Due: Thursday, March 15 (in class)

This assignment gives the opportunity to earn at most 60 extra points toward the first mid-term exam. You will not be able to earn more than the total 150 points available on the exam.

---

1. [30 pts] Consider the following function:

   \[ f(x) = \frac{1 - (1-x)}{x}. \]

   Obviously, if you cancel the 1's in the numerator $f(x) = 1$ for all values of $x$. However if you compute $f(x)$ as written above in MATLAB, it does not return $1$ when $x$ is small. Using MATLAB we can plot $f(x)$ for $x \in [-2\epsilon_m,2\epsilon_m]$ using the following code

   f = @(x) (1- (1-x))./x;
   x = -2:.01:2;
   x = eps*x;
   plot(x,f(x))
   axis([-2*eps 2*eps 0 2])
   title('Plot of $$f(x) = \frac{1-(1-x)}{x}$$','interpreter','latex');
   xlabel('$x$','interpreter','latex');
   ylabel('$f(x)$','interpreter','latex');

   which produces the following image:

   

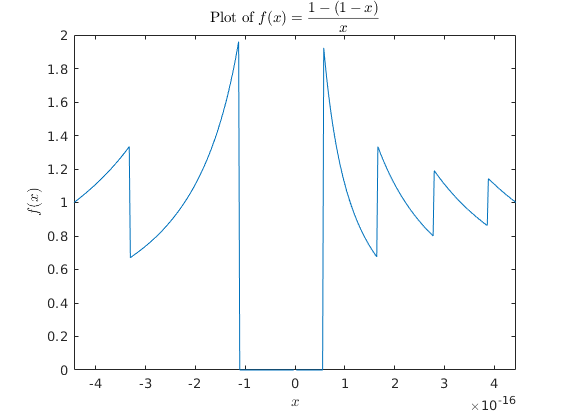
   Please explain why the graph looks like it does. (I suggest testing out $f$ in MATLAB at certain values of $x$).

   In particular please answer the following questions: (5pts each)

   1. Why is $f(x) = 0$ for $0 \leq x < \epsilon_m/4$?

   2. Why is $f(x) = 0$ for $-\epsilon_m/2 < x\leq 0$? Specifically, why is the $f$ zero for twice as long on the left than on the right?

   3. Why does $f(x)$ jump from zero to the value $2$ at around $x = .250001\epsilon_m$?

   4. Why does $f(\epsilon_m) = 1$?

   5. Why does $f$ oscillate around $1$ for $.25\epsilon_m < x < 2\epsilon_m$?

   6. Why are there twice as many oscillations for positive $x$ as there are negative $x$?

2. [15 pts] Suppose that $f(x)$ has infinitely many continuous derivatives on $[a,b]$ and that $\bar{x} \in [a,b]$ is a $n$th order root for $f$, namely

   \[ f(\bar{x}) = 0, \quad f^\prime(\bar{x}) = 0, \quad \ldots,\quad f^{(n-1)}(\bar{x}) = 0,\quad f^{(n)}(\bar{x}) \neq 0. \]

   We want to apply Newton's method to find the root $\bar{x}$. Derive a formula relating the $i+1$th error $e_{i+1} = x_{i+1} - \bar{x}$ for Newton's method to the $i$th error $e_i$, to leading order in $e_i$. What is the corresponding order of convergence?

3. [15 pts] Let

   \[ \mathbf{A} = \begin{bmatrix} 1 & -2 \\ -2 & 3\end{bmatrix} \]

   Answer the following questions.

   1. Find a vector $\mathbf{x}$ such that $\|\mathbf{A}\mathbf{x}\|_{\infty} = \|\mathbf{A}\|_\infty$

   2. Find a vector $\mathbf{x}$ such that $\|\mathbf{A}\mathbf{x}\|_1 = \|\mathbf{A}\|_1$

   3. What are $\kappa_1(\mathbf{A})$ and $\kappa_\infty(\mathbf{A})$ respectively?