Tropical Geometry - Spring 2017
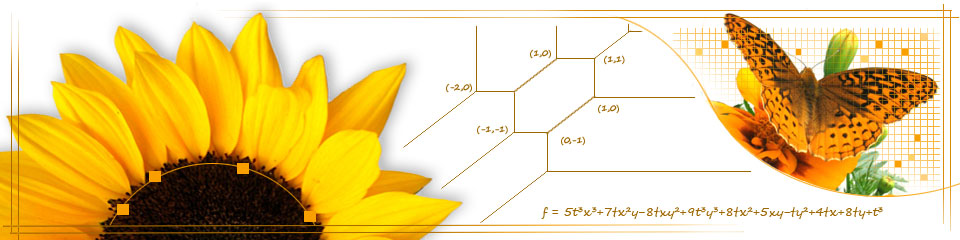
This course will be an introduction to tropical geometry. This is the study tropical varieties which are combinatorial objects (polyhedral complexes) associated to classical algebraic varieties. These objects encode a wealth of information about the original varieties. We will mostly be following the book of D. Maclagan and B. Sturmfels. Topics include: Groebner and Tropical bases, structure of tropical varieties, the fundamental theorem of tropical geometry, tropical linear algebra, matroid theory, toric connections.
Course info
- Lectures: TTh 11:35-12:50
- Classroom: HLH17 113
- Office: 406 DL
Syllabus
You can find the syllabus here.Office hours
If you need help with the course or you have questions regarding the material or the homeworks or you would just want to pick up your homework, please don't hesitate to stop by my office or write me an email. If the time is inconvenient you can arrange an appointment.Office hours: Wednesday 2pm - 3pm
Homework Sets
- Homework Set 1 - due February 14.
- Homework Set 2 - due March 14.
- Homework Set 3 - due April 27.
Schedule
| Lecture # | Date | Topic |
|---|---|---|
| 1 | 01/17 | Intro, tropical arithmetics, valuations |
| 2 | 01/19 | Valuations, varieties, polyhedral geometry |
| 3 | 01/24 | Polyhedral geometry, Groebner basis, term orderings |
| 4 | 01/26 | Groebner basis over fields with valuation, initial ideals |
| 5 | 01/31 | Groebner complexes |
| 6 | 02/02 | Groebner complexes, tropical basis |
| 7 | 02/14 | Tropical varieties, Kapranov's theorem |
| 8 | 02/16 | Kapranov's theorem, tropical varieties over field extensions |
| 9 | 02/21 | The fundamental theorem of tropical geometry |
| 10 | 02/23 | Bieri-Groves |
| 11 | 02/28 | The structure theorem |
| 12 | 03/02 | Multiplicities and balancing |
| 13 | 03/07 | Hyperplane arrangements |
| 14 | 03/09 | Matroids |
| 15 | 03/28 | Dressian, valuated matroids, tropical ideals |
| 16 | 03/30 | Tropical ideals |
| 17 | 04/19 | Tropical ideals, tropical schemes |
| 18 | 04/19 | (guest lecture - Dan Corey) tropical Grassmaniann |
| 19 | 04/25 | Tropicalization of toric varieties |
| 20 | 04/28 | Tropicalization of toric varieties, geometric tropicalization |