Notes
APMA 1650 - Spring 2020
Discrete Probability and Combinatorics
Sample point method
Discrete probability deals with probability when the sample space is discrete, meaning that the the sample space is comprised of a finite number or countable number of elements. In such a case the probability of any event can be written as a (potentially infinite) sum over the probability of elementary events \[ P(A) = \sum_{a \in A} P(\{a\}).\tag{1}\label{1} \]
This allows us to tabulate probabilities in table by listing elements of $S$ along with the corresponding probabilities. The probability of an event $A$ can then be calculated by equation \eqref{1}. This approach is known as the sample point method.
- List the sample space by determining all possible outcomes for an experiment $S = \{s_1,s_2,\ldots\}$.
- Assign probabilities to each simple event, ensuring that $P(\{s_i\}) \geq 0$ and $\sum_i P(\{s_i\}) = 1$.
- Write an event $A$ of interest in terms of simple events.
- Add the probabilities in the event $A$ to compute $P(A)$.
We will illustrate this with several examples.
Example 1 (Fair Coin Toss)
Suppose you flip a fair coin and record the one of the two outcomes as 'heads' (H) or 'tails' (T). In this case the sample space is given by \[ S = \{ H , T\}. \] Since the coin is fair, each outcome is equally likely. Therefore the probabilities are each $1/2$. \[ P(H) = 1/2, P(T) = 1/2. \]
Of course we can spice things up with a couple extra coin tosses.
Example 2 (Three fair coin tosses)
Suppose you flip a fair coin three times and record each of the three outcomes. In this case the sample space of all possible outcomes is \[ \begin{aligned} S &= \{ HHH , HHT, HTH, HTT,\\ &\quad THH, THT, TTH, TTT\}. \end{aligned} \] Since the coin is fair, again each outcome is equally likely. Since there are $8$ outcomes and they must add up to $1$, each outcome has probability $1/8$. We can write this in the form of probability table:
| HHH | HHT | HTH | HTT | THH | THT | TTH | TTT | |
|---|---|---|---|---|---|---|---|---|
| Prob | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
Suppose we want to know what the probability of exactly two heads. This event $A$ is given by \[ A = \{HHT, HTH, THH\} \] The probability is then given by
Example 3 (Roll two fair dice)
Suppose its your turn in Monopoly and you roll two fair dice. In this case you have a couple options for the sample space
- You can record the sum of the two dice and obtain a sample space of \[ S= \{2,\ldots,12\}. \] In this case all of the outcomes are not equally likely
- You can record the values of each consecutive dice roll with the sample space being all possible pairs \[ S = \{(1,1),(1,2),\ldots, (6,6)\}. \] While the sample space is bigger here, it has the benefit that all outcomes are equally likely.
| Die 1 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|---|
| Die 2 | 1 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ |
| 2 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | |
| 3 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | |
| 4 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | |
| 5 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | |
| 6 | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | $\frac{1}{36}$ | |
Since there are 6*6 = 36 possible squares, each outcome being equally likely means that each has a probability of $\frac{1}{36}$.
Using this table, we can now calculate the probabilities that the sum takes values between $2$ and $12$ by adding up the numbers of elements along the diagonals linking two numbers. This gives:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prob | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ |
This tells us, for instance, that $7$ is the most likely sum when rolling two dice.
Combinatorics: the theory of counting
Of course, the examples considered were done in a brute-force manner. Simply exhausting all possible outcomes and leveraging the fact that certain ways of writing the sample space involve equally likely events. If the sample space were much larger (let's say we flip a coin $100$ times), listing the sample space becomes impractical. However, if the outcomes are all equally likely, then we can get away with simply counting the number of outcomes Indeed, for a given finite set $A\subset S$, we denote \[ |A| = \text{ the number of elements in } A. \] If all the outcomes in $S$ are equally likely, then since the probabilities of each outcome must sum up to $1$, we conclude that the probability of each outcome must be $1/|S|$. This given us a general formula for the probability of an event $A$:
This means that in the case of equally likely outcomes, for finite sample spaces we can focus on methods for counting events. Luckily there is a whole branch of mathematics dedicated to counting, known as combinatorics:
- Combinatorics
- The mathematical theory of counting finite structures.
The rule of products
One of the most basic and fundamental tools in combinatorics is what's known as the rule of products, which allows us to think of "building a set" in terms of a series of actions. Specifically:
By iterating the rule of products, we can generalize this method to any number of actions. Roughly speaking, the rule of products allows one to break down a counting problem systematically into a series of actions required to build the set. For example, when counting all of the outcomes of three coin tosses we can think of each coin toss as a separate action with two possible outcomes $H$ or $T$. This means that the number of ways to flip 3 coins is given by \[ 2\cdot 2\cdot 2 = 2^3 = 8. \]
Important
It is important to note that the rule of products is very general and applies even if the number of ways to perform a certain action depends on the action taken before it. This is very useful and is illustrated in the following example.Example 5 (Olympics)
Suppose there are 5 competitors in Olympic speed walking event. How many ways can the gold, silver, bronze medals be awarded?
To answer this, we think of awarding each medal as an action, first we award gold, then silver, then bronze. There are 5 ways to award gold. However once gold is awarded, there are only 4 people left to award the silver to, and then three ways to award the bronze. This means that the total number of ways to award the three medals is \[ 5\cdot 4\cdot 3 = 60 \quad \text{ways}. \]
A more subtle example is the following:
Example 6 (Birthday problem)
Suppose that you select a group of 20. Ignoring leap years so that there are 365 days in a year, how many ways are there for nobody to share the same birthday?
To solve this, we can think about assigning birthdays to each person in the group one by one. For the first person there are 365 choices. However, once they have been assigned a birthday, we cannot repeat it, so there are 364 ways to assign the second person a birthday and so on. Repeating until the last person, we see that there are $365- 19= 364$ ways to assign the last birthday. This gives that there are \[ 365\cdot 364 \cdot 363 \ldots 346 \] ways for no two people to share a birthday. This is a huge number!
Now suppose that all birthdays are equally likely. What is the probability that no two people share the same birthday? If we denote $A$ the event that no two people share the same birthday, then we have just shown that \[ |A| = 365\cdot 364 \cdot 363 \ldots 346. \] Therefore we simply need to determine how big $S$ is. Since $S$ is all the possible ways people can be assigned birthdays regardless of whether people share a birthday, we find \[ |S| = \underbrace{365\cdot 365 \ldots 365}_{20 \text{ times}} = 365^{20}. \] Therefore the probability is \[ P(A) = \frac{|A|}{|S|} = \frac{365\cdot 364 \cdot 363 \ldots 346}{365^{20}} \approx .59. \]
Question:
The birthday problem is often stated as: What is the probability that at least two people share the same birthday?
How is this related to the probability that no two people share the same birthday?
Permutations, combinations and partitions
We note introduce several important counting formulas commonly used in combinatorics.
Permutations
One of the most fundamental ideas in combinatorics is the idea of a permutation of set.
- Permutation
- A permutation of a finite set is ordered arrangement of the elements.
For instance the set $\{a,b,c\}$ has six possible permutations \[ abc, acb, bac, bca, cab, cba. \]
Note
The arrangements $abc$ and $acb$ are distinct permutations. Namely the order matters for permutations.
Of course one can attempt to find all the permutations of a set by writing down all the permutations as we did above. However, this becomes unfeasible when the size of the set is large. Luckily we can be more clever and approach this as we did for the Olympics and Birthday problem by realizing that for the set $\{a,b,c\}$ there are three ways to pick the first element in the permutation, then after that is chosen, two ways to pick the second element, and then one way to pick the last. This gives \[ 3\cdot 2 \cdot 1 = 3! = 6 \] ways to permute the set $\{a,b,c\}$. In general we have:
More generally, it is often the case that we are interested in the number of ways to permute $r$ things out of a set of $n$. This can be thought of in the same way as the total number of permutation, with there being $n$ ways to choose the first element, $n-1$ ways to choose the second, all the way down to $n-(r-1)$ ways to choose the $r$th element. This can be summarized and written in factorial notation as:
Note
We use $P^n_r$ to denote the number of ways to permute $r$ thing out of $n$. However, it is often denoted a number of other ways, for instance \[ {}_nP_r, {}^nP_r, P_{n,r} \text{ or } P(n,r). \]
Example 8
Suppose that Mathematics Magazine, gives a ranking of the top 5 mathematicians in the world. This year they pick the top 5 from a pool of 20 mathematicians. How many ways are there to assign the top 5 rankings to these 20 mathematicians?
Since the ranking must involve different people in each spot, we can see this as the number of ways to permute $5$ things out of $20$, namely there are \[ P^{20}_5 = \frac{20!}{15!} = 1,860,480 \text{ ways}. \]
Combinations
It is often the case that we don't care about the order of elements chosen from a set. In contrast to a permutation, where order matters, a subset where order doesn't matter is known as a combination.
- Combinations
- A combination of size $r$ from a set of $n$ elements is a subset of $r$ elements. The number of such combinations is denoted $C^n_r$ or ${n \choose r}$ (read "n choose r").
For instance, we can list all the possible combinations of $3$ elements out of the set $\{a,b,c,d\}$ as \[ \{a,b,c\}, \quad \{a,b,d\}, \quad \{a,c,d\}, \quad \{b,c,d\}. \] We see then that there are $4$ ways to choose $3$ things from $4$.
As a more systematic approach to determining the number of combinations above, we can first calculate the number of permutations $P^4_3 = 4!/(4-3)! = 24$ of $3$ elements from as set of $4$. However since we don't care about order, this over-counts by all the ways ways that any particular combination of three things can be permuted, which is $3!$. Therefore if we divide by $3!$ we should obtain the total number of ways to choose three things from a set of $4$ without regards to the order, i.e. the number of combinations is \[ \frac{P^4_3}{3!} = \frac{4!}{3!(4-3)!}. \] This is illustrated more precisely in the following table \[ \begin{array}{cc|cc} C^4_3 & & & P^4_3 &\\\hline &&&\\ \begin{array}{c} \{a,b,c\}\\ \{a, b, d\}\\ \{a, c, d\}\\ \{b, c, d\} \end{array} & & & \begin{array}{cccccc} abc & acb & bac & bca & cab & cba\\ abd & adb & bad & bda & dab & dba\\ acd & adc & cad & cda & dac & dca\\ bcd & bdc & cbd & cdb & dbc & dcb \end{array} \end{array} \]
More generally we have,
Note
The quantity ${n\choose r}$ is often referred to as the binomial coefficient since they arise naturally in the expansion of $(x+y)^n$ into a binomial sum$ \[ (x+y)^n = \sum_{i=0}^n {n \choose i} x^iy^{n-i}. \]
Question
Can you verify that the binomial coefficient satisfies Pascal's rule \[ {n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}? \]
Example 9
The following problem appeared in the New-York times recently.
How many triangles are present in the following picture?
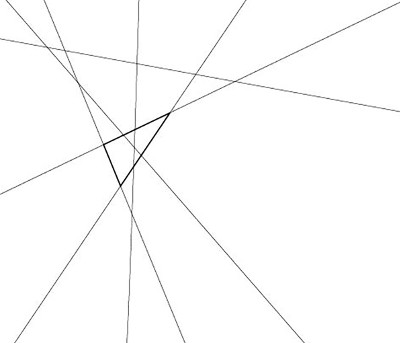
To solve this, we note that there are $6$ lines, that no two lines are parallel and that every intersection only involves two lines. Since a triangle is made of three lines and every three lines in the image make a triangle, we simply need to understand all the ways to choose $3$ lines out of $6$. This is given by \[ {6 \choose 3} = \frac{6!}{3!3!} = \frac{6\cdot 5\cdot 4}{3 \cdot 2} = 20. \] Therefore there are $20$ triangles.
Partitions
The final combinatorial tool we will consider is related to partitions.
- Partition
- A $k$- partition of a set is a collection of $k$ disjoint subsets that make up the set.
It is often the case that we want to know all the possible number of ways to partition a set in $k$ distinct subsets of specific sizes. For instance, consider the set of $7$ elements $\{a,b,c,d,e,f,g\}$ and suppose we wanted to partition it into 3 subsets of sizes $2,4$ and $1$. An example of such a partition would be \[ \{a,b\}, \{c,d,e,f\}, \{g\}. \] To calculate the number of partitions, we can follow a similar strategy to the way we computed the number of combinations. Namely if $N$ is the number of such partitions, we can relate it to the total number of partitions $7!$ of the total set by realizing that the total number of partitions can be obtained by first calculating all possible partitions and the all the possible ways to permute the elements in each partition. Using the rule of products, we obtain the following relation \[ 7! = N \cdot 2! \cdot 4! \cdot 1!. \] Solving for $N$ gives \[ N = \frac{7!}{2! 4! 1!}= 105. \]
In general we obtain the following formula:
Note
The quantity ${n\choose n_1\,n_2\, \ldots n_k}$ is often referred to as the multinomial coefficient as they are a natural extension of the binomial coefficient, namely they describe how to expand a sum of $k$ terms raised to the $n$th power \[ \begin{aligned} &(x_1+x_2 +\ldots + x_k)^n = \\ &\sum_{n_1 + n_2 + \ldots n_k = n}^n {n \choose n_1\,n_2\,\ldots n_k} \prod_{i=1}^k {x_i}^{n_k}.\\ \end{aligned} \]
Example 10
How many unique ways are there to permute the the word "RACECAR"?
This can be seen as a partition problem. Since several letters repeat, the word doesn't change under permutations of each letter type. As such, we view each letter type as a partition of size of the number times that letter appears In this case there are $n= 7$ letters in the word with $k=4$ distinct letters, $n_R = 2$ R's, $n_A = 2$ A's, $n_C = 2$ C's and $n_E = 1$ E. As we have seen before lets try to count the number of unique permutation by trying to systematically build all such words. It helps to imagine that you have $4$ bins with each letter type in it, and you have blank work with $7$ letter slots \[ \cdot \,|\, \cdot \,|\, \cdot \,|\, \cdot \,|\, \cdot \,|\, \cdot \,|\, \cdot \]. You then partition the $7$ blank slots into 4 parts of size $n_R, n_A, n_C$ and $n_E$ respectively and place each letter type in those slots. We know that the number of ways to build such partitions is \[ {7 \choose 2\, 2 \, 2 \, 1} = \frac{7!}{2! 2! 2! 1!} = 630. \] Therefore there are $630$ unique ways to permute "RACECAR".
Example 10
Suppose you are a postal worker and you need to distribute 20 pieces of mail between 4 different mailboxes. Labeling the mailboxes $A-D$, you know that mailbox A has 9 pieces of mail, mailbox B 5 pieces, mailbox C 2 pieces and mailbox D 4 pieces, but you forgot which mail goes where. You decide to randomly distribute the mail between the mailboxes according to how many pieces you know go in each. What is the probability that you get it right?
Since the order inside the mailboxes doesn't matter, the number of possible ways you could distribute the mail is just \[ |S| = {20 \choose 9\, 5\, 2\, 4} = \frac{20!}{9! 5! 2! 4!}. \] Since there is only one way to get it right, we have \[ P(\text{get it right}) = \frac{9! 5! 2! 4!}{20!}. \]
