Homework 1

Due: Thursday 2/8

If you are unfamiliar with MATLAB please see the resources page for a list of references. Also Moler Chapter 1 has a nice introduction to MATLAB.

---

1. Let $f(x) = \ln(1+x)$. Write down the Taylor series around $x=0$ (MacLauren series) for $f(x)$. How many terms in the series are required to estimate $f(0.1)$ with a relative error less than $10^{-5}$.

2. Moler Chapter 1, Exercise 1.38.

3. Consider the function $f(x) = 1-e^{-x}$.

   1. Calculate the condition number $c_f(x)$. Is $f$ ill conditioned or well-conditioned for $x\in[0,1]$? (Hint: use the fact that $(e^{x} - e^{-x})/x \geq 2$)

   2. In MATLAB calculate the unavoidable error of in computing $f(1\times 10^{-6})$, use the eps command for machine epsilon and the exp command.

   3. Compute $f(1\times 10^{-6})$ using the $1-e^{-x}$ formula in MATLAB.

   4. Determine a different formula for $f(x)$ which involves the hyperbolic trig function $\sinh$. Compute $f(1\times 10^{-6})$ using this new formula in MATLAB and the sinh command.

   5. Using arbitrary precision arithmetic one can determine an accurate value of $f(1\times10^{-6})$ to be \[ f(1\times 10^{-6}) \approx 0.99999950000016666662500000833333\times 10^{-6}. \] What is the relative error between what you computed using the two different formulas for $f(x)$? Describe each algorithm as stable or unstable. Why?

4. Consider the function \[ f(x) = \frac{\sqrt{1+x^2} - 1}{x^2}. \] Using MATLAB, we can attempt to plot $f(x)$ near $x=0$ with the following code:

   x = -3:.0001:3;
   x = 1e-7.*x;
   y = (sqrt(1+x.^2) - 1)./x.^2;
   plot(x,y)
   title('Plot of $$f(x) = \frac{\sqrt{1+x^2} - 1}{x^2}$$','interpreter','latex');
   xlabel('$x$','interpreter','latex');
   ylabel('$y$','interpreter','latex');

   This produces the following image:

   

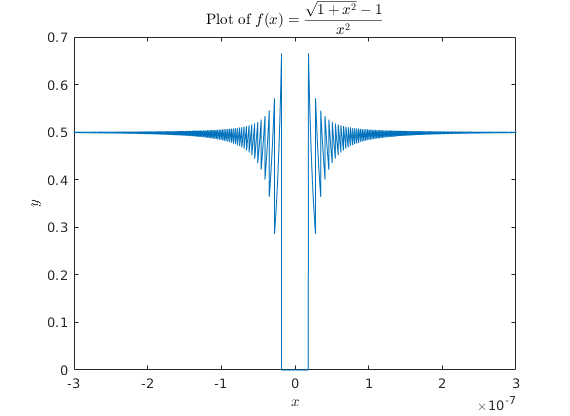
   1. Using L'Hopital's rule, show that \[ \lim_{x\to 0} f(x) = \frac{1}{2}. \]

   2. Why is this not seen in the plot produced by MATLAB? Why does MATLAB run into problems for $x$ in the range $[-10^{-7},10^{-7}]$? Why does MATLAB state $f(x) = 0$ for small values of $x$?

5. Recall the binary representation of a number $x \in [0,1]$ is given by

   \[ x = (.d_1 d_2\ldots )_2 = d_1\cdot 2^{-1} + d_2\cdot 2^{-2} + \ldots, \]

   where $d_i\in \{0,1\}$. Our goal in this problem is to convert a decimal representation to a binary one. Namely, we would like to determine the coefficients $d_1,d_2,\ldots $ associated with a given number $x$.

   Using elementary operations and MATLAB's floor, mod and pow2 functions (type >> help function_name in MATLAB to learn more about any given function) write a formula for the $i$th digit of the binary representation of $x$ in valid MATLAB code (Hint: multiply $x$ by $2^i$ and round to the nearest integer using floor. When is the resulting number even or odd?). Use this to formula to write MATLAB code to determine the first $10$ digits of the binary representation for the following numbers:

   1. $x=10^{-1}$

   2. $x=3^{-1}$

   3. $x=7^{-1}$

   4. $x = 0.314159$

   The output should be a vector of 1's and 0's. For instance $x=.5$ should produce [1 0 0 0 0 0 0 0 0 0].